例 9-1
在石墨炉原子吸收分光光度计上用均匀设计试验法选择测定微量钯的工作条件。已知影响钯吸光度的主要因素有灰化温度(X1)、灰化时间(X2)、原子化温度(X3)和原子化时间(X4)。由原子化机理可知, 灰化温度和原子化温度对吸光度的影响可拟合为二次函数, 即回归方程中应有X12和X32两项。两因素发生在不同时间, 因此不存在交互作用, x1x3项可不列入回归方程; 灰化时间和原子化时间的影响比较复杂, 但也用二次多项式逼近, 忽略其交互作用, 方程中有x22和x42项。加上一次项, 回归方程系数个数为8, 至少应安排9次试验才能求得各系数。根据实际经验选择的各因素的水平值如表1所示。
表 1 因素及水平设计
| 水平代号 | 灰化温度(x1),℃ | 灰化时间(x2),s | 原子化温度(x3),℃ | 原子化时间(x4),s |
| 1 | 200 | 10 | 2500 | 4 |
| 2 | 350 | 18 | 2600 | 5 |
| 3 | 500 | 26 | 2700 | 6 |
| 4 | 650 | 34 | 2800 | 7 |
| 5 | 800 | 42 | 2900 | 8 |
| 6 | 950 | 50 | 3000 | 9 |
| 7 | 1100 | |||
| 8 | 1250 | |||
| 9 | 1400 | |||
| 10 | 1550 | |||
| 11 | 1700 | |||
| 12 | 1900 |
用混合水平的均匀设计表安排试验, 试验方案和结果见表2。
表 2 试验方案和结果(括号外的数字为水平编号, 括号内的数字为各因素的水平值)
| 试验序号 | 灰化温度(x1),℃ | 灰化时间(x2),s | 原子化温度(x3),℃ | 原子化时间(x4),s | 吸光度(y),AU |
| 1 | 1( 200) | 3(26) | 4(2800) | 5(8) | 0.151 |
| 2 | 2( 350) | 6(50) | 2(2600) | 4(7) | 0.113 |
| 3 | 3( 500) | 3(26) | 6(3000) | 2(5) | 0.199 |
| 4 | 4( 650) | 6(50) | 3(2700) | 1(4) | 0.116 |
| 5 | 5( 800) | 2(18) | 1(2500) | 6(9) | 0.091 |
| 6 | 6( 950) | 5(42) | 5(2900) | 4(7) | 0.142 |
| 7 | 7(1100) | 2(18) | 2(2600) | 3(6) | 0.099 |
| 8 | 8(1250) | 5(42) | 6(3000) | 1(4) | 0.135 |
| 9 | 9(1400) | 1(10) | 4(2800) | 6(9) | 0.128 |
| 10 | 10(1550) | 4(34) | 1(2500) | 5(8) | 0.029 |
| 11 | 11(1700) | 1(10) | 5(2900) | 3(6) | 0.116 |
| 12 | 12(1900) | 4(34) | 3(2700) | 2(5) | 0.016 |
注: 本例子采用的混合水平的均匀设计表的水平排列方式与方开泰先生所著《均匀设计与均匀设计表》, 科学出版社, 1994 中给出的混合水平的均匀设计表U12(12X63)的水平排列方式不同, 特此说明。
均匀设计2.10版启动后界面如下:
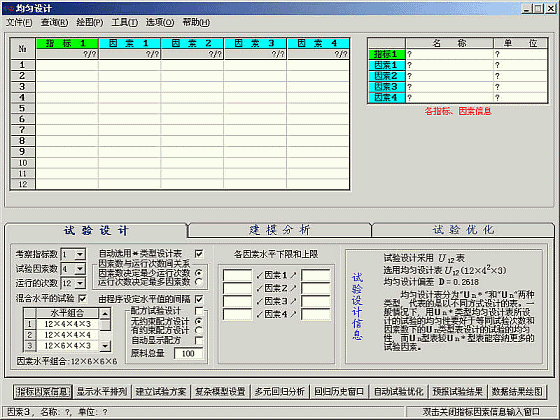
在“试验设计”栏目依次选择“考察指标数为1,试验因素数为4,运行的次数(即试验次数)为12。

选中“混和水平的试验选框”,选择水平组合为12X6X6X6。
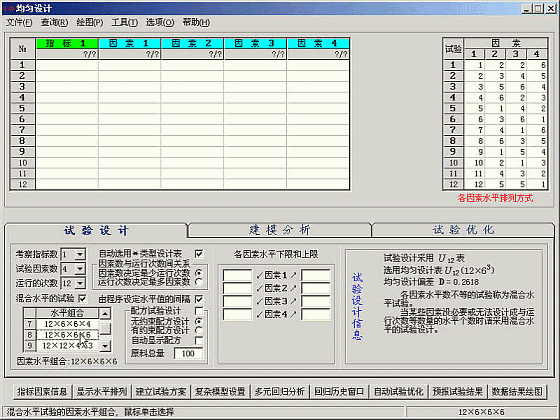
点击“指标因素信息”按钮,显示指标因素信息

依次输入指标和因素的名称、单位

本例子采用的混合水平的均匀设计表的水平排列方式与方开泰先生所著《均匀设计与均匀设计表》, 科学出版社, 1994 中给出的混合水平的均匀设计表U12(12X63)的水平排列方式不同。故需要手动输入指标因素的数据。

数据录入完毕后最好马上存储一下数据,以免误操作后遗憾 :)
点击“多元回归分析”按钮

回归模型设置选中“二次项”(默认也是这个选项)
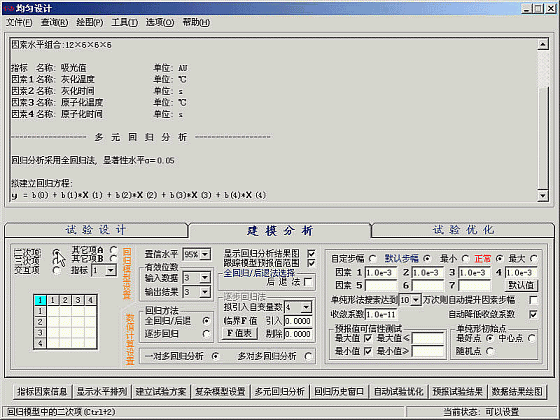
分别选中1X1、2X2、3X3、4X4的交互项,请注意上方“拟建立回归方程”会实时变化。

选中1X1的交互项时,拟建立的回归方程如下:

选中所有2次项的交互项

此时拟建立的回归方程如下:

点击“多元回归分析”按钮

弹出对话框,不用理他,这只是由于“预报值可信性测试”栏目没有设置值的原因。

确定后可以拖动滚动条查看软件给出的运行结果,如下:
------------------ 试 验 基 本 信 息 ------------------
指标数: 1, 因素个数: 4, 运行次数: 12
试验设计选用均匀设计表 U12(12×4×4×3)
因素水平组合:12×6×6×6
指标 名称: 吸光值 单位: AU
因素1名称: 灰化温度 单位: ℃
因素2名称: 灰化时间 单位: s
因素3名称: 原子化温度 单位: ℃
因素4名称: 原子化时间 单位: s
------------------- 多 元 回 归 分 析 -------------------
回归分析采用全回归法, 显著性水平α=0.05
拟建立回归方程:
y = b(0) + b(1)*X(1) + b(2)*X(2) + b(3)*X(3) + b(4)*X(4) + b(5)*X(1)*X(1) + b(6)*X(2)*X(2) + b(7)*X(3)*X(3) + b(8)*X(4)*X(4)
回归系数 b(i):
b(0)= 0.384
b(1)= 1.00e-5
b(2)=-3.32e-3
b(3)=-3.53e-4
b(4)= 1.42e-2
b(5)=-3.58e-8
b(6)= 4.03e-5
b(7)= 9.85e-8
b(8)=-1.08e-3
标准回归系数 B(i):
B(1)= 0.110
B(2)=-0.948
B(3)=-1.26
B(4)= 0.507
B(5)=-0.837
B(6)= 0.704
B(7)= 1.93
B(8)=-0.502
复相关系数 R=0.9972
决定系数 R^2=0.9944
修正的决定系数 R^2a=0.9846
样本容量N=12, 显著性水平α=0.05, 检验值Ft=66.62,
临界值F(0.05,8,3)=8.845, Ft>F(0.05,8,3),
回归方程显著。
剩余标准差 s=7.17e-3
回归系数检验值:
t检验值(df=3):
t(1)= 0.4588
t(2)=-3.476
t(3)=-0.6007
t(4)= 1.222
t(5)=-3.486
t(6)= 2.588
t(7)= 0.9223
t(8)=-1.216
F检验值(df1=1, df2=3):
F(1)= 0.2105
F(2)= 12.08
F(3)= 0.3609
F(4)= 1.493
F(5)= 12.15
F(6)= 6.699
F(7)= 0.8506
F(8)= 1.478
偏回归平方和 U(i):
U(1)=1.08e-5
U(2)=6.20e-4
U(3)=1.85e-5
U(4)=7.66e-5
U(5)=6.24e-4
U(6)=3.44e-4
U(7)=4.37e-5
U(8)=7.59e-5
偏相关系数 ρ(i):
ρ1,2345678= 0.2561
ρ2,1345678=-0.8950
ρ3,1245678=-0.3277
ρ4,1235678= 0.5764
ρ5,1234678=-0.8955
ρ6,1234578= 0.8311
ρ7,1234568= 0.4700
ρ8,1234567=-0.5745
各方程项对回归的贡献(按偏回归平方和降序排列):
U(5)=6.24e-4, U(5)/U=2.28%
U(2)=6.20e-4, U(2)/U=2.27%
U(6)=3.44e-4, U(6)/U=1.26%
U(4)=7.66e-5, U(4)/U=0.280%
U(8)=7.59e-5, U(8)/U=0.277%
U(7)=4.37e-5, U(7)/U=0.160%
U(3)=1.85e-5, U(3)/U=6.77e-2%
U(1)=1.08e-5, U(1)/U=3.95e-2%
第1方程项[X(1)]对回归的贡献最小, 对其进行显著性检验:
检验值F(1)=0.2105, 临界值F(0.05,1,3)=10.13,
F(1)≤F(0.05,1,3), 此因素(方程项)不显著。
残差分析:

在“试验设计”栏目依次选择“考察指标数为1,试验因素数为4,运行的次数(即试验次数)为12。

选中“混和水平的试验选框”,选择水平组合为12X6X6X6。

点击“指标因素信息”按钮,显示指标因素信息

依次输入指标和因素的名称、单位

本例子采用的混合水平的均匀设计表的水平排列方式与方开泰先生所著《均匀设计与均匀设计表》, 科学出版社, 1994 中给出的混合水平的均匀设计表U12(12X63)的水平排列方式不同。故需要手动输入指标因素的数据。

数据录入完毕后最好马上存储一下数据,以免误操作后遗憾 :)
点击“多元回归分析”按钮

回归模型设置选中“二次项”(默认也是这个选项)

分别选中1X1、2X2、3X3、4X4的交互项,请注意上方“拟建立回归方程”会实时变化。

选中1X1的交互项时,拟建立的回归方程如下:

选中所有2次项的交互项

此时拟建立的回归方程如下:

点击“多元回归分析”按钮

弹出对话框,不用理他,这只是由于“预报值可信性测试”栏目没有设置值的原因。

确定后可以拖动滚动条查看软件给出的运行结果,如下:
------------------ 试 验 基 本 信 息 ------------------
指标数: 1, 因素个数: 4, 运行次数: 12
试验设计选用均匀设计表 U12(12×4×4×3)
因素水平组合:12×6×6×6
指标 名称: 吸光值 单位: AU
因素1名称: 灰化温度 单位: ℃
因素2名称: 灰化时间 单位: s
因素3名称: 原子化温度 单位: ℃
因素4名称: 原子化时间 单位: s
------------------- 多 元 回 归 分 析 -------------------
回归分析采用全回归法, 显著性水平α=0.05
拟建立回归方程:
y = b(0) + b(1)*X(1) + b(2)*X(2) + b(3)*X(3) + b(4)*X(4) + b(5)*X(1)*X(1) + b(6)*X(2)*X(2) + b(7)*X(3)*X(3) + b(8)*X(4)*X(4)
回归系数 b(i):
b(0)= 0.384
b(1)= 1.00e-5
b(2)=-3.32e-3
b(3)=-3.53e-4
b(4)= 1.42e-2
b(5)=-3.58e-8
b(6)= 4.03e-5
b(7)= 9.85e-8
b(8)=-1.08e-3
标准回归系数 B(i):
B(1)= 0.110
B(2)=-0.948
B(3)=-1.26
B(4)= 0.507
B(5)=-0.837
B(6)= 0.704
B(7)= 1.93
B(8)=-0.502
复相关系数 R=0.9972
决定系数 R^2=0.9944
修正的决定系数 R^2a=0.9846
变量分析表
| 变异来源 | 平 方 和 | 自 由 度 | 均 方 | 均 方 比 |
| 回 归 | U=2.74e-2 | K=8 | U/K=3.42e-3 | F=66.62 |
| 剩 余 | Q=1.54e-4 | N-1-K=3 | Q/(N-1-K)=5.13e-5 | |
| 总 和 | L=2.75e-2 | N-1=11 |
剩余标准差 s=7.17e-3
回归系数检验值:
t检验值(df=3):
t(1)= 0.4588
t(2)=-3.476
t(3)=-0.6007
t(4)= 1.222
t(5)=-3.486
t(6)= 2.588
t(7)= 0.9223
t(8)=-1.216
F检验值(df1=1, df2=3):
F(1)= 0.2105
F(2)= 12.08
F(3)= 0.3609
F(4)= 1.493
F(5)= 12.15
F(6)= 6.699
F(7)= 0.8506
F(8)= 1.478
偏回归平方和 U(i):
U(1)=1.08e-5
U(2)=6.20e-4
U(3)=1.85e-5
U(4)=7.66e-5
U(5)=6.24e-4
U(6)=3.44e-4
U(7)=4.37e-5
U(8)=7.59e-5
偏相关系数 ρ(i):
ρ1,2345678= 0.2561
ρ2,1345678=-0.8950
ρ3,1245678=-0.3277
ρ4,1235678= 0.5764
ρ5,1234678=-0.8955
ρ6,1234578= 0.8311
ρ7,1234568= 0.4700
ρ8,1234567=-0.5745
各方程项对回归的贡献(按偏回归平方和降序排列):
U(5)=6.24e-4, U(5)/U=2.28%
U(2)=6.20e-4, U(2)/U=2.27%
U(6)=3.44e-4, U(6)/U=1.26%
U(4)=7.66e-5, U(4)/U=0.280%
U(8)=7.59e-5, U(8)/U=0.277%
U(7)=4.37e-5, U(7)/U=0.160%
U(3)=1.85e-5, U(3)/U=6.77e-2%
U(1)=1.08e-5, U(1)/U=3.95e-2%
第1方程项[X(1)]对回归的贡献最小, 对其进行显著性检验:
检验值F(1)=0.2105, 临界值F(0.05,1,3)=10.13,
F(1)≤F(0.05,1,3), 此因素(方程项)不显著。
残差分析:
残差分析表
| № | 观 测 值 | 回 归 值 | 观测值-回归值 | (回归值-观测值)/观测值×100(%) |
| 1 | 0.151 | 0.154 | -3.00E-03 | 1.99 |
| 2 | 0.113 | 0.112 | 1.00e-3 | -0.885 |
| 3 | 0.199 | 0.192 | 7.00e-3 | -3.52 |
| 4 | 0.116 | 0.114 | 2.00e-3 | -1.72 |
| 5 | 9.10e-2 | 9.60e-2 | -5.00E-03 | 5.49 |
| 6 | 0.142 | 0.144 | -2.00E-03 | 1.41 |
| 7 | 9.90e-2 | 9.93e-2 | -3.00E-04 | 0.303 |
| 8 | 0.135 | 0.139 | -4.00E-03 | 2.96 |
| 9 | 0.128 | 0.123 | 5.00e-3 | -3.91 |
| 10 | 2.90e-2 | 2.48e-2 | 4.20e-3 | -14.5 |
| 11 | 0.116 | 0.119 | -3.00E-03 | 2.59 |
| 12 | 1.60e-2 | 1.62e-2 | -2.00E-04 | 1.25 |
------------------ 回 归 分 析 结 束 ------------------
选择“试验优化”条目


按默认选择“计算方法”为“单纯形法”,“优化方向”为“寻最大值”,“单纯形初始点”为“最好点”。设定上限设定值和下限设定值为实验范围,如x1为200和1900。指标方向寻最大值时输入1,寻最小值时输入-1,此处为寻最大值,输入1。


点击“自动优化实验”按钮


等待计算结果


弹出对话框,不予理睬。


得出优化的实验条件
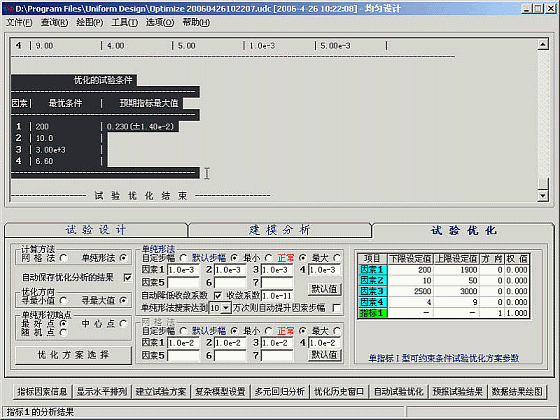

可以拖动滚动条查看软件运行结果,如下:
------------------ 试 验 条 件 优 化 ------------------
试验优化方法: 单纯形法
条件优化设置列表
| 因 素 | 上 界 | 下 界 | 初始值 | 初始步幅 | 初始步长 | 收敛系数 |
| 1 | 1.90e+3 | 200 | 500 | 1.0e-3 | 1.70 | 1.0e-11 |
| 2 | 50.0 | 10.0 | 26.0 | 1.0e-3 | 4.00e-2 | |
| 3 | 3.00e+3 | 2.50e+3 | 3.00e+3 | 1.0e-3 | 0.500 | |
| 4 | 9.00 | 4.00 | 5.00 | 1.0e-3 | 5.00e-3 |



